In this post, I will try to explain what the idea of gradient descent is, which is the basis of a lot of machine learning algorithms, especially neural networks. I will try to explain this in the easiest way, but feel free to grab your long-lost calculus book along the way. :)

Neural Network

In short, a neural network is a bunch of neurons that are connected together through different layers. A neuron can be simply thought as a thing that holds a number, which typically ranges from 0 to 1. The first layer consists of neurons representing the inputs, while the last layer contains neurons representing outputs. In between, there could be layers called hidden layers, which is a huge subject for further discussions.

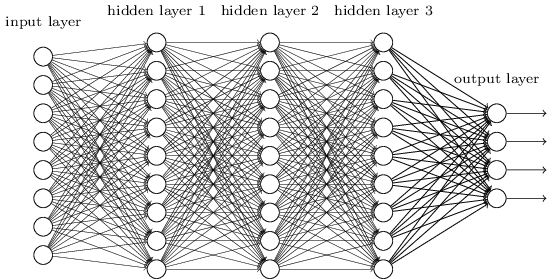
The connections of neurons between two layers are essentially weights, which can also be intuitively interpreted as the strength of the strings. As we have values for neurons in input layers, the value of a neuron in the following layers is calculated as the weighted sum of values of all neurons from the previous layer. In order to flexibly keep the values in a reasonable range, a bias term is added to the weighted sum in order to control inactivity. Remember that for most of the time, we want to keep the range between 0 and 1. For this to be done, the values need to be squashed. A common function that does this is the Sigmoid function, as used in the Logistic regression. And this part of the process is called the activation. To summarize, a nueral network works simply in the following way.

• Time the weights
• Add the bias
• Activate

Gradient Descent

As we understand what a neural network is, you may ask how does the learning part works. Supurisingly, this is not like rocket science, but it is actually just calculus (even worse LOL!). If you want to tell the machine that it is doing something wrong and to correct that, you need some sort of measurement for the machine to understand. Basically, it comes to finding the minima of a certian function, which is named the cost function (like the residual sum of squares used in OLS). In order to do this in a more generalized way, we start at a random point, and then tries to find the direction where the cost function decreases the fastest. In fact, the generic gradient descent does not guarantee that the local minima you land in is the smallest possible value of the cost function. If you are familar with multi-variable calculus, you would know that the gradient of a function gives the direction of the steepest ascent, which is the direction to increase the function most quickly. Thus, taking the negative of that gradient gives the direction to decrease the function most quickly. The algorithm for minimizing the function is simply to compute the gradient direction, then take a small step towards the opposite direction, and just repeat that over and over.

So now if you are still feeling not completely sure how a neural network works, this feeling is 100% right. I have not yet covered the algorithm named backpropagation for computing this gradient efficiently, which is the heart of how a neural network learns. And that is what will be covered in the next post.

Thank you for your reading. :)